Funkce v Excelu – využití se zaměřením na matematiku

 

Otázka: Funkce v Excelu – využití v úlohách se zaměřením na matematiku

Předmět: Informační a komunikační technologie

Přidal(a): Petr Kuděj

 

PŘEDMATURITNÍ ROČNÍKOVÁ PRÁCE

Funkce v Excelu – využití v praktických úlohách se zaměřením na středoškolskou matematiku

 

ANOTACE

Obsahem této práce je využití funkcí v programu Microsoft Excel ve středoškolské matematice. V práci jsou uvedeny jak jednodušší, základní funkce, tak i pokročilé příklady tvorby grafů, či použití doplňku Řešitel. Jsou zde uvedeny možné problémy při používání funkcí programu Microsoft Excel. Práce vychází z učiva matematiky na středních školách a vyšších stupních gymnázií. Výsledkem je zhodnocení používání tohoto programu v matematice a také sbírka úloh na procvičení těchto funkcí v praxi.

Klíčová slova: Excel, funkce, matematika, grafy, Řešitel, problémy, využití

 

ANNOTATION

This work deals with the use of functions in Microsoft Excel in high school mathematics. There are easy and basic functions in this work, just like hard and complicated ones, for example in creating graphs or use of Solver add-on. There are also listed problems of using functions in Microsoft Excel. This work is based on the mathematics curriculum on high schools. The result of this work is an evaluation of using Microsoft Excel in mathematics and also a collection of practical exercises of these functions.

 

Keywords: Excel, functions, mathematic, graphs, Solver, problems, usage

 

Obsah

• Úvod
• Struktura práce
  • Základní matematické funkce v Excelu
  • Goniometrické funkce
• Funkce sinus
• Funkce kosinus
• Funkce tangens
• Funkce kotangens
• Grafy goniometrických funkcí
  • Kvadratická funkce
  • Funkce s absolutní hodnotou
  • Řešitel

• O doplňku Řešitel
• Použití Řešitele
• Přidání doplňku do Excelu
• Řešení matematických problémů
  • Problémy při využívání těchto funkcí
• Diskuze
• Závěr

 

Úvod

Práce je zaměřena na program Microsoft Excel, především na jeho funkce a jejich využití ve středoškolské matematice. Práci jsem si vybral na základě mých znalostí tohoto programu a jeho funkcí a se zájmem o osobní rozvoj v tomto směru. Poukazuje na rozmanité využití tohoto programu. V praktických úlohách a názorných ukázkách tato práce vysvětlí některé z mnoha funkcí, které program Microsoft Excel nabízí a objasní možnosti jejich použití v praxi nebo při vyučování.

Při tvorbě této práce byla využita nejnovější verze programu, a to Microsoft Excel 2016 v českém jazyce. Některé funkce nesou jiný název v anglické modifikaci. Většina funkcí je obsáhlá i v předchozích verzích, ovšem nelze zaručit, že budou fungovat i v novějších verzích tohoto programu.

Práce se především kromě jiného zaměřuje na matematické funkce. V tomto případě není myšleno slovní příkaz v Excelu, nýbrž látku, která se probírá na středních školách. Do této kapitoly spadají například goniometrické funkce, kvadratické funkce, či funkce s absolutní hodnotou. Kromě toho je zde popsán i doplněk Řešitel. Práce obsahuje také nedostatky a chyby těchto funkcí

Cílem je ukázat možnosti využívání programu Microsoft Excel ve školách při vyučování a možnosti praktického využívání funkcí, dále pak seznámit začínající uživatele programu o jeho možnostech. Práce počítá se základní znalostí Excelu, například práci s buňkami, orientaci v kartách apod. a se základní znalostí terminologie.

 

Struktura práce

Hlavním zdrojem při vytváření práce byly mé vlastní zkušenosti, které jsem získal převážně už v předchozích letech od mého otce, Ing. Milana Kuděje. Delší dobu jsem pozoroval široké možnosti využití Excelu, a proto jsem se rozhodl shrnout tyto možnosti do této práce.

Informace získané od něj jsem dále rozšířil o publikaci Microsoft Excel 2013: podrobná uživatelská příručka od Jiřího Barilly, Květuše Sýkorové a Pavla Simra [1]. V této příručce jsem se začal zajímat kromě jiného o funkce a jejich využití. V tomto ohledu už byl zběhlý můj starší bratr Lukáš Zeman, který mě kromě veškeré práce se softwarem i hardwarem naučil používání funkcí v Excelu.

Dalším hlavním zdrojem, který jsem použil hojně, byla podpora Microsoft. Ne vždy jsem nalezl to, co jsem potřeboval v české verzi této nápovědy, proto jsem musel hledat i v cizojazyčné podpoře, případně na různých fórech. Přesto na některé mé otázky jsem nenalézal odpověď, proto jsem ji zkoušel nalézt sám procházením různých možností programu.

Internet mi byl velmi důležitým zdrojem pro hledání informací, a kromě nápovědy od společnosti Microsoft, která tento program vytvořila, jsem často využíval osobní stránku Pavla Lasáka s názvem Jak na Excel [4]. Je zde popsána téměř každá funkce, včetně ukázky použití.

Látku, kterou rozebírám této práci velmi podrobně, tedy matematické funkce, jsem vybral z důvodu, že jsme tuto problematiku na vyšším stupni gymnázia probírali. Vybíral jsem tedy podle učiva na naší škole převážně v kvintě a sextě.

Při čtení práce se čtenář nejdříve dozví, jak pracovat se základními funkcemi, později pokročilými a jak tyto funkce využívat a kombinovat, dále přiblížím tvorbu grafů pro matematické funkce, část práce je také věnována doplňku Řešitel a na závěr představím problémy s těmito funkcemi a zhodnocení využití programu Microsoft Excel v praxi.

 

1. Základní matematické funkce v Excelu

Nejprve je důležité znát základní funkce a práci s nimi, popis funkce a k čemu tyto funkce v Excelu slouží. Funkce se dá jednoduše popsat jako automat na kávu, do kterého se vloží peníze, to představuje určitý vstup a výsledkem a výstupem je káva. [2] Takto funguje funkce. Je potřeba zadat vstup a funkce počáteční hodnotu pozmění podle daného vzorce. Každá funkce musí mít za sebou napsané závorky. Do těch se píší parametry funkcí a hodnoty se kterými má funkce pracovat. Závorky je nutné napsat i v případě, když funkce nemá žádné parametry.

V Excelu je možný zápis dvou typů obsahu buňky. Buď je možné zadat text, který se zobrazí tak, jak je zapsán, či vzorec, který se po potvrzení zobrazí jako výsledek daného vzorce. Rozdíl v zápisu spočívá v tom, že při psaní vzorce je nutné napsat před text znaménko =. Vzorcem může být například sčítání, odčítání atd. Stejně se zapisují i funkce (nejen matematické), které jsou také typem vzorce.

Například pro sčítání 2 čísel stačí napsat do buňky: „=a+b“, kdy písmena značí buď určité číslo, nebo odkaz na buňku s číslem. Odkaz se zapíše formou souřadnic. Každý sloupec má své písmeno a každý řádek své číslo. Tohoto se používá například v případě, kdy se vstupní hodnoty mění.

Mezi základní matematické funkce v Excelu patří bezesporu funkce SUMA() [4], která sečte všechny vstupy, které lze buď oddělit v závorce za funkcí středníkem, nebo pokud je hodnot více, je možné vybrat oblast, ve které funkce SUMA() sečte všechny hodnoty. Oblast se označí jako „A1:A4“. V tomto případě jsou vybrány buňky A1, A2, A3, A4. V kombinaci s touto funkcí vypadá vzorec například takto: „=SUMA(A2;B2)“. V tomto případě se zobrazí součet buněk A2 a B2 (viz Obr.1). Nebo takto: „=SUMA(A2:A4)“, kdy se zobrazí díky pomlčce součet buněk A2, A3 a A4.

Další základní funkcí je například funkce GDC(), která vrátí největší společný dělitel. Používá se následovně: „=GDC(A1;A2)“. Poté je důležitá funkce ODMOCNINA(), která vrátí druhou odmocninu čísla. Po zadání „=ODMOCNINA(A1)“ se zobrazí druhá odmocnina hodnoty v buňce A1. Například po zadání čísla 9 do parametrů funkce se zobrazí hodnota 3. Mezi základní funkce patří také funkce KDYŽ(), nejedná se ale o matematickou funkci, nýbrž o logickou. V závorkách se nachází 3 parametry. Nejprve je zde uvedena podmínka, u které se zjišťuje, zda je splněna, například „A1>0“. Konkrétně tato podmínka ověřuje, zda je hodnota v buňce A1 větší než nula. Dalším parametrem, který se oddělí středníkem, je výstup v případě, kdy je podmínka splněna. Může se vypsat buď číslo, text, nebo případně může proběhnout nějaká funkce. Text musí být zadán vždy v uvozovkách kvůli rozlišení datového typu, funkce se zapíše bez uvozovek. Následující parametr, který je opět oddělen středníkem určuje, co se stane, pokud podmínka není splněna. Celý vzorec může vypadat například takto: „=KDYŽ(A1>0;“Číslo je větší než nula“;“Číslo je menší nebo rovno nule“)“.

Nemusí se ovšem jednat jen o čísla, lze prověřit, zda daná buňka obsahuje konkrétní text, to by vypadalo například takto: „A1=“text“. Dále také funkce nemusí být jen výstupem z funkce, ale i v podmínce. Například při zjištění, zda je součet nějakých dvou čísel větší než jiné číslo (funkce SUMA()), nebo jestli je konkrétní buňka prázdná, či vyplněná. To se nastaví funkcí JE.PRÁZDNÉ(). Do parametru této funkce patří odkaz na buňku, u které se prověří, zda je prázdná, v tom případě je podmínka pravdivá, nebo zda prázdná není, v tom případě je podmínka nepravdivá. V parametrech funkce lze funkce kombinovat a například po zjištění, že je podmínka pravdivá, provést další funkci, například opět funkci KDYŽ() a zjistit platnost další podmínky.

 

2. Goniometrické funkce

2.1. Funkce sinus

Funkce sinus je jedna z nejpoužívanějších goniometrických funkcí a v učivu středoškolské matiky zaujímá velkou kapitolu. Použití nalézá například při sčítání vektorových fyzikálních veličin nebo při přípravách technických výkresů. V praxi může jít například o měření výšky budov nebo v astronomii vzdálenosti blízkých hvězd. V matematice je v pravoúhlém trojúhelníku je definována jako poměr protilehlé odvěsny ku přeponě.

Práce v programu Microsoft Excel je s touto funkcí snadná. Existuje pro to jednoduchá funkce, která se značí stejně jako v matematice, tedy SIN(). Do parametrů funkce, mezi závorky, patří údaj v radiánech, ke kterému se vypočítá sinus.

V tomto případě se budou užitečné dvě další funkce. Tou první je funkce PI(), která Vrátí číslo 3,14159265358979, matematickou konstantu , s přesností na 14 desetinných míst. [4] Vhodná je tedy při zapisování hodnot v radiánech, jako je například  nebo . Dál se s ním dá pracovat stejně jako s číslem, můžeme například do parametrů funkce sinus napsat „=PI()/2“, což odpovídá devadesáti stupňům. Program nám následně vrátí hodnotu 1.

Častým problémem při psaní desetinných čísel či velkých čísel v řádu tisíců a větších může být ten, že každému vyhovuje jiný typ oddělovače. Ten je možný nastavit v okně Možnosti, který se nachází na kartě Soubor. Dále je třeba kliknout na Upřesnit a zrušit označení pole Používat oddělovače ze systému. V následujících polích lze nastavit nové oddělovače.

Následující funkcí je v tomto případě RADIANS(), ta převede číslo v závorce ze stupňů do radiánů. Snadné využití nalézá při hledání sinu netabulkových hodnot, jako je například 10 stupňů. Funkce vypadá v tomto případě takto: „=RADIANS(10)“. Celou tuto funkci je nyní možno zapsat do parametru sinus. To bude vypadat následovně: „=SIN(RADIANS(10))“. Program vrátí hodnotu sinus pro 10 stupňů. Tvorba grafu je vysvětlena v odstavci 2.5 Grafy goniometrických funkcí.

Nemusí se ovšem jednat jen o funkci . Do parametrů matematické funkce se dá spoustu přidat, funkce může ve výsledku vypadat například takto: „=SIN((x+1)^2)“ (x značí číslo, nebo odkaz na buňku s číslem). V matematice by se tato funkce značila jako .

V praxi nalézá tato funkce využití například při používání sinové věty. Ta vypadá následovně: . Pro použití v Excelu je nutné převést neznámou na jednu stranu, tedy například pokud není známa strana a, bude vypadat vztah takto: . Pokud úhel  , úhel  a strana  , bude vzorec v aplikaci vypadat takto: „=5/SIN(RADIANS(30))*SIN(RADIANS(60)).

Samozřejmě program Microsoft Excel nabízí i funkci, pro funkci inverzní k sinus. Arkus sinus má v Excelu označení ARCSIN(). V matematice je definována jako: . Do parametrů se vypíše příslušný sinus a jako výsledek se zobrazí hodnota úhlu. Například: „=ARCSIN(1)“. Do buňky se vypíše číslo v radiánech. K převodu do stupňů je potřeba využít funkci DEGREES(). Například po zadání: „=DEGREES(ARCSIN(1))“ zobrazí program 90.

 

2.2 Funkce kosinus

Kosinus je další goniometrická funkce, která má velmi blízko k sinus a dá se využít ke stejným účelům. V pravoúhlém trojúhelníku je definována jako poměr přilehlé odvěsny ku přeponě. V matematice se tato funkce značí cos.

V programu Microsoft Excel se pracuje s touto funkcí stejně jako s funkcí sinus. Pro zjištění kosinu úhlu se používá funkce COS(). Do parametrů se opět zapíše daný úhel v radiánech, ke kterému můžeme použít již dřív zmíněné funkce PI() a RADIANS(). Jejich používání je vysvětlené v předchozím odstavci 2.1. Funkce sinus. Vytvoření grafu je popsáno v odstavci 2.5 Grafy goniometrických funkcí.

Nemusí jednat pouze o jednoduchý tvar , ale jde s ním dále pracovat a přidávat parametry. Jak je ukázáno v odstavci 2.1. Funkce sinus (viz Obr.2). Obdobným způsobem jako se používá v Excelu sinová věla, lze použít k výpočtu i kosinová věta.

I u této funkce je možnost funkce inverzní, což je funkce, která odpovídá . Zapisuje se v podobě funkce ARCCOS(). Do parametrů funkce mezi závorky patří hodnota kosinu úhlu, který chceme zjistit, takže funkce může vypadat například takto: „=ARCCOS(0,5)“ (arkuskosinus jedné poloviny). Hodnota se zobrazí v radiánech. Je tedy vhodné použít funkci DEGREES(). Tato funkce převádí radiány na stupně. Po zadání funkce „=DEGREES(ARCCOS(0,5))“ se v buňce vypíše 60, neboť kosinus šedesáti stupňů je 0,5.

 

2.3. Funkce tangens

Další goniometrická funkce se nazývá tangens. Je definována v pravoúhlém trojúhelníku jako poměr odvěsny protilehlé ku odvěsně přilehlé a její použití je tedy v praxi stejné jako u předchozích goniometrických funkcí. I její označení jako funkce v Excelu je stejné jako matematické funkce a to TG(). Do parametrů opět patří hodnota x, tedy úhel v radiánech. K tomu slouží funkce PI() a RADIANS(), jejíchž použití a význam jsou vysvětleny v odstavci 2.1. Funkce sinus.

S funkcí se dá dále pracovat a různě upravovat, například do tvaru „=2*TG(4*x)^2“. Konkrétně tento tvar vyjadřuje funkci .

U tangens existuje také v Excelu funkce pro inverzní funkci arkustangens. Tato funkce je definována takto: . V Excelu se zapisuje jako ARCTG(). Do parametrů funkce patří opět tangens úhlu, který má Excel zjistit. Funkce vrátí výsledek v radiánech, tudíž velmi užitečná je funkce DEGREES(), která převede radiány na stupně. Příklad může vypadat například takto: „=DEGREES(ARCTG(1))“. Jako výsledek této funkce se zobrazí 45, nýbrž tangens čtyřiceti pěti stupňů je 1.

 

2.4 Funkce kotangens

Poslední goniometrická funkce, která je definována v pravoúhlém trojúhelníku jako poměr odvěsny přilehlé ku odvěsně protilehlé, se nazývá kotangens a její využití v praxi je stejné jako u už výše uvedených goniometrických funkcí. V programu Microsoft Excel má trochu jiné označení než v matematice a to COT(). Pracuje se s ní ale stejně jako s výše uvedenými goniometrickými funkcemi. Do parametrů funkce, tedy do závorky, patří hodnota x, pro kterou tato funkce vypočítá kotangens. Vstupním formátem jsou opět radiány, tudíž vhod přijdou funkce PI() a RADIANS(). Vysvětleny jsou tyto dvě funkce již výše v odstavci 2.1. Funkce sinus.

Do funkce lze přidat další argumenty, nezůstat tak jen u základního tvaru „=COT(x)“ a tak vytvořit například tuto funkci: „=4*COT(2*x)^3“.

Také u této funkce se dá v Excelu pracovat s její inverzní hodnotou. Arkus kotangens se dá definovat jako  a zapisuje pomocí funkce ACOT(). Pracuje se s ní stejně jako s předchozími inverzními funkcemi a to tak, že do parametrů funkce patří údaj o hodnotě kotangens zjišťovaného úhlu. Program vrátí hodnotu arkus kotangens v radiánech. Proto je užitečná funkce DEGREES(), která převede radiány do stupňů. Funkce pak může vypadat například takto: „=DEGREES(ACOT(1))“. Program vrátí hodnotu 45. Kotangens čtyřiceti pěti stupňů je totiž 1.

 

2.5 Grafy goniometrických funkcí

V případě, že chceme vytvořit graf, budeme potřebovat vytvořit tabulku, kde jeden řádek, či sloupec bude udávat hodnoty x a druhý hodnoty y. V případě goniometrických funkcí patří do jednoho řádku stupně, pro které chceme zobrazit jejich sinus v grafu. Může se jednat i o radiány, v tom případě není nutné použít funkci RADIANS(). Pokud zadáme stupně je potřeba tuto funkci použít. Nejvhodnější je zadávat stupně po deseti. Do druhého řádku vypíšeme funkci sinus, kosinus, tangens nebo kotangens, kde parametr bude obsahovat odkaz na buňku s hodnotou x v horním řádku, popřípadě převod ze stupňů na radiány. Takže napsaná funkce může vypadat například takto: „=SIN(RADIANS(A3))“. V buňce A3 je původní hodnota x ve stupních. Toto stejný postup platí pro všechny hodnoty, které se zobrazí v grafu. Není nutnost se omezovat na  , je možné funkci rozepsat například do tvaru „=2*SIN(RADIANS(3*A3))“. Pokud je použita tato funkce, zobrazí ve výsledku Excel graf funkce .

Pro urychlení slouží zatažení za dolní pravý okraj buňky, který zkopíruje funkci do další buňky a příslušně změní její parametry, tedy pokud je v buňce před posunutím: „=SIN(RADIANS(A3))“, tak po posunutí doprava se do další buňky zkopíruje funkce: „=SIN(RADIANS(A4))“. Tento způsob lze využít i při zapisování hodnot x. Například po zapsání čísla 10 a do vedlejší buňky 20, je možné označit tyto 2 buňky a tažením doprava postupně kopírovat do buněk 30, 40, 50, atd., tažením doleva se bude naopak hodnota o deset snižovat, tedy 0, -10, -20 atd.

Dalším krokem je kartě Vložit vybrat graf spojnicový. Při kliknutí pravým tlačítkem na zatím prázdný obdélník, který vznikl, se zobrazí menu, ze kterého je třeba vybrat položku Vybrat data (viz Obr.3). Poté v levém sloupci vybrat tlačítko Přidat a smazat v druhém řádku „={1}“ a místo toho označit řádek, kde jsou hodnoty sinus. Po kliknutí na OK je ještě potřeba kliknout na tlačítko Upravit v pravém sloupci, kde vybereme řádek s hodnotami x. Výsledkem po potvrzení bude příslušný graf, tedy sinusoida, kosinusoida, tangentoida nebo kotangentoida.

 

3. Kvadratická funkce

V každé kvadratické funkci se vyskytuje alespoň jedna neznámá s druhou mocninou. Obecně kvadratické rovnice mají plno využití, jako jsou různorodé vzorce, například vzorec při výpočtu obvodu kružnice, obsahu čtverce, či použití v Pythagorově větě. V programu Microsoft Excel existují dvě možnosti pro vypočítání kvadratických rovnic a pro práci s kvadratickými funkcemi.

V prvním případě není potřeba použít funkce Excel, ale stačí stisknutí Klávesy Alt Gr a klávesy š. Vypíše se stříška, která značí, že za tímto znakem se bude nacházet právě exponent. Například kvadratická funkce:  vypadat v Excelu takto: „=2*x^2“ (na místo x patří buď konkrétní číslo, nebo odkaz na buňku s číslem). Pozor na to, že stříška se nejprve nevypíše, zobrazí se až poté, co je za ni napsán nějaký znak, v tomto případě exponent.

Druhou možností je použít funkci POWER(). Tuto funkci je možné použít i v případě kubických a dalších rovnic, kde se nachází mocnina. Do parametrů této funkce patří dvě položky, tou první je hodnota, se kterou se bude dál pracovat, která bude buď ve tvaru čísla, či odkazu na buňku s číslem a tou druhou položkou je exponent. V případě kvadratické funkce se jedná o číslo 2. Tyto dva argumenty jsou odděleny středníkem, který se na klávesnici nachází vlevo na klávesnici nad klávesou Tab. Již výše zapsaná matematická funkce bude v programu Microsoft Excel vypadat po použití této funkce následovně: „=2*POWER(x;2)“ (neznámá x zde nahrazuje opět konkrétní číslo, či odkaz na jinou buňku). Funkci lze využít i pro výpočty odmocnin. Třetí odmocnina je vlastně mocnina na 1/3. Takže pro druhou odmocninu lze využít „=POWER(x;1/2)“, pro třetí „=POWER(x;1/3)“. [4]

K vytvoření grafu jsou potřeba dva řádky nebo sloupce. První řádek bude obsahovat hodnoty x a druhý řádek hodnoty y. V druhém řádku bude zapsána konkrétní funkce odkazující na řádek horní s příslušnou hodnotou x, například: „=2*POWER(A2;2)“ (původní hodnota x je v buňce A2). Následně je nutné vybrat na kartě Vložit bodový graf s vyhlazenými spojnicemi, po kliknutí na něj se zobrazí možné akce a po vybrání Vybrat data je nutné přidat do levého sloupce (řady) hodnoty y, tedy druhý řádek. Pravý sloupec je třeba upravit tak, aby zde byly hodnoty prvního řádku s hodnotami x. Po stisknutí OK se graf zobrazí. Stejným způsobem se dají vytvářet i exponenciální grafy a rovnice.

 

4. Funkce s absolutní hodnotou

Absolutní hodnota v matematice se značí |x|. Program Microsoft Excel ovšem neumí tento znak přečíst. Proto se pro absolutní hodnotu používá funkce ABS(). Do parametrů funkce patří číslo, či odkaz na buňku s číslem x. Funkce může vypadat například takto: „=ABS(-5)“. Po stisknutí Enter vrátí Excel číslo 5.

Graf se tvoří stejně jako u ostatních funkcí. Nejprve je potřeba první řádek, do kterého patří hodnoty x a následně druhý řádek, kde se vypíší hodnoty y tak, že se zde použije funkce ABS(), kde v parametru bude uveden místo čísla x odkaz na příslušnou hodnotu v horním řádku. Funkce pak může vypadat ve druhém řádku takto: „=ABS(A2)“. V tomto případě je v parametru funkce odkaz na buňku A2 s výchozí hodnotou x. V případě absolutní hodnoty je nejlepší použít x-ové hodnoty mezi -5 a 5. Následně je potřeba vybrat na kartě Vložit graf bodový, u absolutní hodnoty s rovnými spojnicemi. Po kliknutí na prázdný graf pravým tlačítkem myši se zobrazí menu a po kliknutí na Vybrat data je nutné vybrat tlačítko Přidat. Místo hodnoty „={1}“, která je napsaná ve druhém řádku je potřeba označit řádek s hodnotami y a potvrdit pomocí OK. Následně v pravém sloupci je pro správné popsání x-ových hodnot potřeba kliknout na Upravit a vybrat první řádek s hodnotami x a kliknout opět na OK. Zobrazí se výsledný graf.

I v tomto případě lze použít tlačítko v pravém dolním rohu buňky, které při posouvání kopíruje, případně upravuje obsah buňky a vkládá do vedlejších. V prvním řádku se dá využít tak, že stačí napsat číslo -5 a vpravo od této hodnoty číslo -4, označit tyto dvě buňky a tažením doprava se budou čísla přičítat. Do dalších polí se vloží postupně -3, -2, -1, 0… Ve druhém řádku lze tato možnost využít tak, že po zapsání jedné funkce, například „=ABS(A3)“, se po zatažení tlačítkem v pravém dolním rohu buňky doprava funkce zkopíruje, pozmění se její obsah a vloží se do vedlejší buňky, tam bude vypadat takto: „=ABS(A4)“.

Absolutní hodnota ve formě funkce ABS() lze v Excelu použít nejen jako samostatná funkce, ale lze ji spojit s jakýmikoliv dalšími funkcemi. Je možné ji například skombinovat s goniometrickými nebo kvadratickými funkcemi. Výsledná funkce pak může vypadat například takto: „=ABS(POWER(SIN(2x);2)+1)“. Jedná se o funkci.

 

5. Řešitel

5.1. O doplňku Řešitel

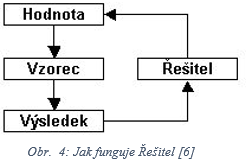
Řešitel je doplněk aplikace Microsoft Excel a používá se pro analýzu dat (viz Obr. 4). Slouží k nalezení konkrétní hodnoty, maxima, či minima daného vzorce. Nejlépe jde představit tato funkce na grafech matematických funkcí, kde pomocí tohoto doplňku lze najít pro funkci její maximum, minimum a určit konkrétní y pro dané x. Doplněk pracuje s účelovou funkcí, s proměnnou modelu a s omezujícími podmínkami. Řešitel ve srovnání s běžnými vzorci funguje přesně obráceně: ze zadané hodnoty výsledku zjišťuje potřebnou vstupní hodnotu (Obr.4). Tuto úlohu není možné vyřešit jedním krokem, a proto Řešitel postupuje iteračně: po zadání výchozího odhadu zjišťované hodnoty a hodnoty, kterou má vzorec produkovat se výpočet opakuje tak dlouho, až se výsledek vzorce liší od zadaného výsledku méně, než je nastavená přesnost. Tento postup má však (jako každý přibližný výpočet) jedno úskalí: výpočet nemusí ve všech případech vést k cíli. [6] Přesnost je možné nastavit po kliknutí na tlačítko Možnosti. Tato přesnost je použita i u zjištění přesnosti splnění podmínek. V tomto okně lze také nastavit maximální počet iterací a maximální čas, ve kterém bude Řešitel hledat řešení. Řešitel využívá 3 metody řešení, Gradientní, Simplexovou a Evoluční algoritmus. GRG Nonlinear neboli Gradientní metoda složí k řešení hladkých nelineárních problémů, metoda LP Simplex neboli Simplexová metoda, složí k řešení lineárních problémů a metoda Evolutionary neboli Evoluční algoritmus, slouží k řešení nehladkých problémů. Nejčastěji postačí Gradientní, či Simplexová metoda.

 

5.2. Použití Řešitele

5.2.1. Přidání doplňku do Excelu

Tím, že je Řešitel doplněk, není vždy součástí základního nastavení Excelu a je často skryt. Stejně jako ostatní doplňky, je potřeba ho v nastavení zobrazit. Nastavením jsou v Excelu konkrétně myšleny Možnosti. Ty se nachází po kliknutí do levého horního rohu na kartu Soubor v levém sloupci úplně dole. Po kliknutí se zobrazí tabulka Možnosti aplikace Excel. Doplňky včetně Řešitele se nachází na záložce Doplňky. V dolní části je potřeba vybrat v rozevíracím poli spravování doplňků Excel a následně kliknout na Přejít. Poté zaškrtnout čtvereček u doplňku Řešitel (viz Obr.5) a potvrdit tlačítkem OK. V tuto chvíli je hotovo a doplněk se přidal na kartu Data pod záložku Analýza.

 

5.2.2. Řešení matematických problémů

V první řadě je potřeba vytvořit tabulku a vzorec, se kterým bude Řešitel pracovat. V tabulce musí být uvedeny hodnoty, které se mohou měnit, ty budou uvedeny v Řešiteli pod názvem proměnné buňky. Například v případě výpočtu maxima matematické funkce bude proměnná buňka obsahovat číslo x. Do této buňky je vhodné napsat odhad na výslede. Řešitel si většinou poradí i s prázdnou buňkou, ale ne vždy. Samotnému programu to velmi ulehčí práci. Účelová funkce bude v tomto případě y. V této buňce musí být zapsána konkrétní funkce, vzorec. Pokud zde bude jen číslo, nelze Řešitel použít. V buňce y může být například „=SIN(RADIANS(A3))“, což odpovídá vzorci . A3 je odkaz na buňku s hodnotou x a funkce RADIANS() je zde proto, aby bylo možné zadat x ve stupních.

Kliknutím na tlačítko Řešitel na kartě Data a v záložce Analýza, se zobrazí okno Parametry Řešitele. V prvního řádku s názvem Účelová funkce se bude nacházet odkaz na buňku s číslem, u které má Řešitel najít maximum, minimum, či konkrétní hodnotu. V dalším řádku je potřeba vybrat, zda Řešitel bude hledat konkrétní hodnotu, či maximum nebo minimum. V případě hledání konkrétní hodnoty je pro tuto hodnotu určeno pole v pravé části, s přednastavenou hodnotou „0“. Do pole Proměnné modelu patří odkaz na buňky, které se budou měnit. Pole Omezující podmínky je určeno pro podmínky, které Řešitel musí dodržet při řešení problému. Například při určení minima jakékoliv matematické funkce může být omezující podmínkou interval této funkce. Podmínka se přidá stiskem Přidat. Následně se do levého sloupce nastaví hodnota k porovnání, uprostřed se zvolí relační znaménko a vpravo bude vypsána hodnota se kterou se buňka bude porovnávat. Doporučuje se používat v obou případech odkaz na buňku, jelikož se tak mohou podmínky měnit a model nastavení zůstává stejný. Mezi další možnosti patří podmínka, že číslo na levé straně musí být celé, či binární. Další volbou, která zde lze změnit je, zda má Řešitel počítat i se zápornými čísly, nebo jen s kladnými. Pokud jen s kladnými, bude políčko s názvem Nastavit podmínky nezápornosti zaškrtlé. Pokud má Řešitel počítat i se zápornými čísly, je potřeba tuto možnost odškrtnout. Metody řešení jsou vysvětleny v dolní části okna, ale nejčastěji stačí použít Gradientní metodu. Už stačí jen kliknout na Řešit a Řešitel zobrazí výsledek. Parametry Řešitele vynulujeme tak, že v dialogu Parametry Řešitele klepneme na tlačítko Vynulovat vše. Dialog Microsoft Excel se nás zeptá, jestli chceme vynulovat všechny možnosti a vybrané buňky v Řešiteli. [1] Doplněk nabízí také možnost uložení model nastavení před vyřešením. To se provede stiskem Načíst nebo uložit, kde stačí vybrat prázdnou buňku (pod kterou je další místo, model zabere více než jeden řádek) a stisknout Uložit. V opačném případě, kdy je potřeba model nahrát, je opět nutné kliknout na Načíst nebo uložit, dále vybrat oblast buněk, kam byl model uložen a kliknout na Načíst.

Po vyřešení nabídne Excel možnost uchovat řešení, či obnovit původní hodnoty. Tím se vrátí zpět řešení a zobrazí se předchozí hodnoty buněk. Dále je možnost sestavit podrobnější výsledek a postup, jak Řešitel postupoval. Sestava se vytvoří na novém listu. Jako poslední lze nastavit, zda se má opět zobrazit okno Parametry Řešitele, pro změnu či nastavení nového postupu řešení.

Příkladem pro využití tohoto doplňku může být například firma vyrábějící 3 typy produktů s různou výrobní a prodejní cenou a je potřeba zjistit kolik výrobků od každého druhu je potřeba vyrobit pro nejvyšší zisk, či pro zisk konkrétní hodnoty.  Ve vybrané buňce, která poslouží jako Účelová funkce se zobrazí výsledek, buňky s počtem vyrobených kusů budou vypsány do pole s názvem Proměnné modelu a do omezujících podmínek můžeme zahrnout například omezený počet všech výrobků, či omezený čas (v tomto případě je třeba zadat potřebný čas pro vyrobení jednotlivých výrobků).

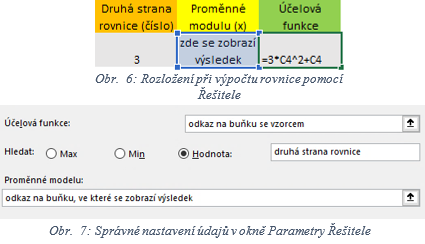
Samozřejmě lze touto metodou řešit i různé matematické rovnice s jednou neznámou (viz Obr. 6). Jedna strana bude zapsaná do buňky sloužit v Řešiteli jako Účelová funkce. Na této straně musí být všechna x. Místo x je ale potřeba zadat odkaz na prázdnou buňku, kde se po vyřešení zobrazí výsledná hodnota x. Účelová funkce může vypadat například takto: „=3*C4^2+C4“, což odpovídá matematickému zápisu . V parametrech Řešitele je nutné zvolit hledat hodnotu a zadat číselnou hodnotu druhé strany rovnice. Do pole Proměnné modelu patří odkaz na buňku s číslem x, v tomto případě A2 (viz Obr. 7) Do Omezujících podmínek může být vložen například interval, jehož elementem musí být hodnota x. Dále je potřeba nastavit, zdali se má počítat i s možnými zápornými čísly, či jen s kladnými (včetně nuly). Stačí následně kliknout na Řešit a Řešitel zobrazí výsledek.

 

6. Problémy při využívání těchto funkcí

Přesto, že Excel je ve všech směrech velmi užitečný i zde se nachází chyby, které mohou zkomplikovat práci s ním. Tyto chyby vyplývají z limitů datových typů. Excel pro výpočet například kosinu devadesáti stupňů používá takový algoritmus, který nevrátí hodnotu 0, ale 6.123233995736766e-17. Jedná se o velmi malé číslo, jen nepředstavitelně blízké nule. A čím je to způsobeno? Funkce kosinus v Excelu, tedy COS(), počítá primárně s radiány a ať už je v parametru funkce (v závorkách) napsaná hodnota v radiánech, či ve stupních, převedena do radiánů pomocí funkce RADIANS(), využívá v obou případech Excel hodnotu . Hodnotu nekonečného čísla. Takové číslo musí být tedy někdy zaokrouhleno, neboť program pochopitelně nedokáže zobrazit nekonečné číslo, ani s ním počítat. Počet platných číslic je v programu Excel omezen na 17 desetinných míst [3]. Poslední číslo je tedy zaokrouhleno a při výpočtu kosinu devadesáti stupňů, tedy , nevyjde výsledek přesně nula. Podobný problém se vyskytuje i u dalších goniometrických funkcí, kde tabulková hodnota je rovna nule. Závažnější problém se vyskytuje u funkce tangens a u devadesáti stupňů. Tato hodnota není správně definována. Avšak funkce „=TG(PI()/2)“ nebo „=TG(RADIANS(90))“ vrátí hodnotu 1,63246E+16. Je to velmi vysoké číslo a tato chyba je způsobena opět hodnotou . Lze to odvodit od definice tangens, která vypadá takto: . Navazuje to na problém s funkcí kosinus. Kosinus devadesáti stupňů je správně nula, přesto Excel nevrátí nulu, ale velmi malé číslo. Nulou dělit nelze, ale tímto malým číslem ano.

Tyto funkce mohou být problematické při tvorbě grafu. Především tangens. U funkce kosinus je toto číslo tak malé, že to vypadá, že se jedná přesně o nulu. Ovšem u funkce tangens je problém ten, že tangens devadesáti stupňů je v Excelu tak vysoké číslo, které celý graf zničí. Je tedy potřeba číslo 90 vynechat. Při volbě x začít od hodnoty -80 a jako poslední zadat hodnotu 80. Je nutné dát si také pozor u zadání grafu, zda ve funkci není uvedeno například 2x, kde by vznikl problém na čtyřiceti pěti stupních, či například u funkce , neboť by zde nebyla tato funkce definována. K podobnému problému dochází i u funkce kotangens. Nejedná se ale o chybu. Kotangens 0 není definován, proto musí uživatel zvolit správný interval, jehož elementem je x. V případě nepozměněné funkce  je potřeba mít x omezené intervalem , v prvním řádku tak budou hodnoty 10, 20, 30…170. Hodnoty 0 a 180 by nahlásily chybu.

 

Diskuze

Excel je program dělaný pro editaci velkých souborů, vytváření rozsáhlých seznamů a tabulek. Co se týče programu jako takového, je to bezpochyby nejvyužívanější a funkčně nejobsáhlejší tabulkový procesor, již od devadesátých let. [5] A stejně tak pestré jsou možnosti jeho využití v matematice. Má velkou výhodu v orientaci, neboť se vším, co se do tabulky napíše se dá později manipulovat, měnit polohu či obsah, dále pomocí jednoduchých funkcí a snadných a lehce pochopitelných vzorců dají spočítat i složité příklady, které by bez tohoto programu zabrali mnohem více času. Navíc je možnost mít předpřipravenou tabulku pro řešení určitých problémů, například sinové věty a při dalším použití jen zadat do konkrétních buněk hodnoty a pomocí vzorců, které jsou uloženy už z předchozího použití, se zobrazí výsledek.

Nevýhodou může být nutnost znalosti všech potřebných funkcí a zjišťování údajů, které jsou na první pohled jasné, přesto je Excel potřebuje pro další výpočty a je nutné vložit složitý vzorec. Dále se vyskytuje při používání tohoto programu problém s náčrty. Některé slovní úlohy je velmi obtížné řešit bez obrázku. Ten je samozřejmě možný vytvořit z tvarů dostupných v aplikaci, ovšem to zabere hodně času a načrtnout situaci na papír je mnohem rychlejší. I takové úlohy jsou na ukázku zařazeny do přiložené sbírky úloh.

Na druhou stranu jsou skvělou možností v tomto programu grafy. I přesto, že jsou zde problémy v některých grafech, je jich jen pár a dají se snadno obejít, viz odstavec Problémy při využívání těchto funkcí. S ostatními grafy Excel nemá žádný problém a zobrazí i složitější. Další důvod, způsobující oblíbenost tohoto programu je propojení s ostatními aplikacemi z kancelářského balíku Microsoft Office. Tabulku či graf vytvořený v Excelu je pak snadné převést do Wordu či PowerPointu.

Excel nemusí vyhovovat všem, velmi záleží na přístupu uživatele a mnozí zvolí podle nich lehčí variantu řešení pomocí papíru a kalkulačky, než aby se dozvěděli něco nového a ulehčili si jejich budoucí práci. Microsoft Excel je program potřebný v téměř každé firmě. Kromě matematiky může být Excel využíván u jednotlivce jako jednoduchý seznam filmů, přehled o příjmech nebo jako tabulka na sledování stavu účtů a plánování výdajů.

 

Závěr

Ve své práci popisuji jednotlivé funkce v Excelu vyplývající z učiva matematiky na středních školách a na vyšším stupni víceletých gymnáziích. Porovnávám použití tohoto programu při řešení matematických problémů s řešením tradičním, za použití kalkulačky, tužky a papíru.

Svých cílů jsem dosáhl a objasnil jsem, proč si myslím, že je používání programu Microsoft Excel v praxi užitečné. Doporučil bych každému, aby se seznámil se základy této aplikace, neboť její rozmanitost je obrovská a během studia informatiky na středních školách bych této problematice věnoval více času. Tato rozmanitost se ovšem neustále vyvíjí a Microsoft brzy přinese novou verzi tohoto programu, která přidá opět nové funkce a nová využití.

V práci nejsou vypsané všechny funkce, které lze v matematice využít, celý přehled matematických funkcí je snadno dohledatelný na české podpoře společnosti Microsoft, se zaměřením na Excel se jedná o tuto stránku: https://support.office.com/cs-cz/excel.

K práci jest přílohou sbírka úloh uložena na přiloženém CD, obsahující příklady na procvičení funkcí, popsaných v této práci, připravena volně k použití pro studijní účely, především na gymnáziu Nad Kavalírkou.

 

Seznam použité literatury

1. BARILLA, Jiří, Pavel SIMR a Květuše SÝKOROVÁ. Microsoft Excel 2013: podrobná uživatelská příručka. Brno: Computer Press, 2013. ISBN 978-80-251-4114-4, s. 256-258 (upraveno)
2. Co je to funkce. Matematika.cz [online]. Brno: Nová média, 2014 [cit. 2018-05-12] (upraveno). Dostupné z: https://matematika.cz/co-je-to-funkce
3. Datové typy v datových modelech – Excel. Microsoft [online]. Washington: Microsoft, 2018 [cit. 2018-05-12] (upraveno). Dostupné z: https://support.office.com/cs-cz/article/datov%C3%A9-typy-v-datov%C3%BDch-modelech-e2388f62-6122-4e2b-bcad-053e3da9ba90
4. LASÁK, Pavel. Matematické funkce – MS EXCEL. Jak na Excel [online]. Lasák, 2017 [cit. 2018-05-12] (upraveno). Dostupné z: http://office.lasakovi.com/excel/funkce/ms-excel-funkce-matematicke/
5. PEMBERTON, J D; ROBSON, A J. Spreadsheets in business. In: “Industrial Management & Data Systems“ [online]. 2000, “’100“'(8), 379-388 [cit. 2016-12-26]. Dostupné z databáze: ProQuest Central. ISSN 0263-5577
6. Řešitel a Hledání řešení. NaPočítači.cz [online]. Praha: Dashöfer Holding, 2018 [cit. 2018-05-13]. Dostupné z: https://www.napocitaci.cz/33/resitel-a-hledani-reseni-uniqueidmRRWSbk196FNf8-jVUh4EibDXKDRp3-E-RwhBOXZcJI/
7. Z vlastního archivu 2018: Snímek z aplikace Microsoft Excel

 

Seznam obrázků

• Obr.  1: Příklad využití funkce SUMA() na sčítání 2 čísel
• Obr.  2: Zápis funkce  do Excelu
• Obr.  3: Okno pro výběr zdrojových dat
• Obr.  4: Jak funguje Řešitel [6]
• Obr.  5: Správně vybraný doplněk Řešitel
• Obr.  6: Rozložení při výpočtu rovnice pomocí Řešitele
• Obr.  7: Správné nastavení údajů v okně Parametry Řešitele

 

Seznam příloh

• Příloha č. 1: Sbírka úloh – přiložena na CD
• Příloha č. 2: Řešení sbírky úloh – přiložena na CD